在計量標準技術報告、校準和測量能力(CMC)、計量標準周期性溯源時,穩定性(長期穩定性和短期穩定性)是一個極其重要的參量,同時也是在不確定度評定過程中極易被忽視的一個分量。
查閱諸如JJF 1059.1-2012《測量不確定度評定與表示》、計量技術規范及其附錄中的不確定度評定示例、與不確定度評定的有關論文等大量文獻資料,并且在1033、CNAS現場評審的經歷總結后發現,鮮有人對穩定性所引入的不確定度分量予以考慮。相反地,在一些國際重要測量或量值比對中,穩定性引入的不確定度是必須考慮的分量之一,這種差異顯然與不確定度評定原則“不重復不遺漏”相違背。
圖1 2018年APMP在絕對壓力量值比對的穩定性圖
測量儀器保持其計量特性隨時間恒定的能力。亦可說測量儀器的計量特性隨時間不變化的能力,亦或是抵抗時間變化的能力。
測量儀器產生不穩定的因素有很多,主要原因是其元器件的老化、零部件的磨損以及使用頻次、貯存條件、維護工作不仔細等引起的。
穩定性可以進行定量的表征,主要是確定計量特性隨時間變化的關系。通常可以用這兩種方法:用計量特性的某個量發生規定的變化所需經過的時間;或用計量特性經過規定的時間所發生的變化量來進行定量表示,即:
y2—規定時間段結束時(或本次周檢)的實際值或變化量;
y1—規定時間段開始時(或上次周檢)的實際值或變化量。
實際上,如果使用這些計量標準進行量值傳遞時,穩定性引起的量值變化大多數只知其變化范圍,而不知其具體變化量,故不能將其當作不確定度分量予以評定,因此極易被忽視。類似的案例很多,這里我們以砝碼、量塊為例展開討論,且此二者在相應的計量檢定規程中對穩定性亦有明確要求。
JJG 99-2022砝碼檢定規程5.3.6對穩定性有如下要求:在規定的準確度范圍內,任何一個質量標稱值為m0的單個砝碼,其相鄰兩個檢定周期的檢定結果不得超過該砝碼最大允許誤差的1/3。
如圖2所示,在2023年溯源完成后,如果以相鄰兩個檢定周期的檢定結果之差作為該砝碼的年穩定性,使用F1等級200g的砝碼開展檢定或校準工作時,穩定性引入的不確定度分量為
如果按照穩定性的極限值(允差)來評定穩定性引入的不確定度分量,使用F1等級200g(MPE:±1.0mg)的砝碼開展檢定或校準工作時,穩定性引入的最大的不確定度分量不超過
u(mδ)=1/3×1.0mg/√3=0.19mg
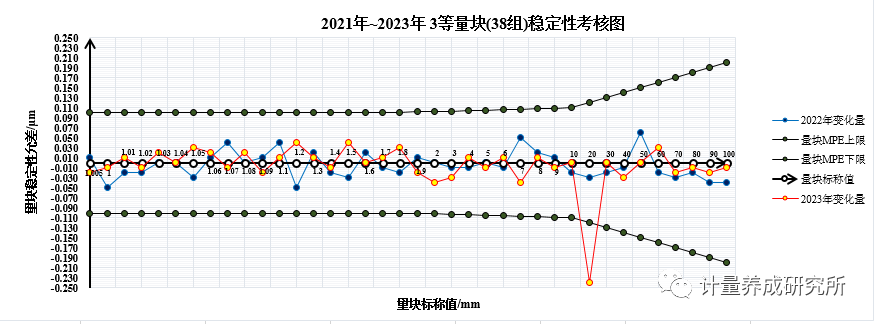
JJG 146-2011量塊檢定規程7.3.11對穩定性有如下要求:在不超過4個檢定周期,穩定性lA應符合表13的規定。
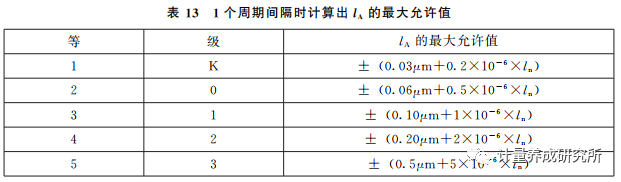 圖4 量塊穩定性最大允許值
如圖5所示,在2023年溯源完成后,如果以相鄰兩個檢定周期的檢定結果之差作為該砝碼的年穩定性,使用3等100mm的量塊開展檢定或校準工作時,穩定性引入的不確定度分量為
如果按照穩定性的極限值(允差)來評定穩定性引入的不確定度分量,使用3等100mm(MPE:±0.2μm)的量塊開展檢定或校準工作時,穩定性引入的最大的不確定度分量不超過
圖4 量塊穩定性最大允許值
如圖5所示,在2023年溯源完成后,如果以相鄰兩個檢定周期的檢定結果之差作為該砝碼的年穩定性,使用3等100mm的量塊開展檢定或校準工作時,穩定性引入的不確定度分量為
如果按照穩定性的極限值(允差)來評定穩定性引入的不確定度分量,使用3等100mm(MPE:±0.2μm)的量塊開展檢定或校準工作時,穩定性引入的最大的不確定度分量不超過
u(lδ)=1/3×0.2μm /√3=0.04μm
以上砝碼和量塊的案例可見,計量標準的穩定性越差(最差不超過其允差ΔS),其引入的不確定度分量越大([0,ΔS/√3]區間之間)。按照經驗統計,在某些實際評定場景中,穩定性引入的不確定度分量u與合成標準不確定度uc之比最大超過2/3(u/uc≥2/3)之多。如果在不確定度的評定過程中忽視這一分量,將對整個不確定度評定的嚴正性及量值傳遞的可靠性產生重要影響。
因此,在這里呼吁從事計量工作及修訂計量技術規范的人員,穩定性引入的不確定度分量不應被忽視,它可以很小甚至為零,但是不能遺漏這一分量。
3 穩定性識別方法及建議
根據以上討論分析,可采用以下方法對由穩定性引入的不確定度予以評定。
在無法給出特定時間段(溯源周期)內量值變化的計量標準,雖然可知其分布區間,但不知其特定時間段的變化量,可以使用其該時間段內的穩定性允差(最大允許誤差ΔS)作為分量,即:
ΔS—穩定性允差限。
如果穩定性引入的量值變化可以被識別(ys=y2-y1),則可將其作為穩定性引入的不確定度予以評定,即:
(1)銷售前的計量標準器,生產廠進行過長期的穩定性考察,給出了該標準隨時間變化量值亦隨之變化的有關信息(如量值、校準曲線等):
(2)國內外標準、計量技術規范、說明書或是其他技術資料提供的信息;
(3)根據歷年多次溯源證書的數據(如控制曲線圖)進行分析;
(5)實驗室多次檢定或校準后的量值(短期穩定性)變化估計;
(7)由經驗估計出穩定性。
(2)已掌握了穩定性變化的特點、規律、趨勢以及適當的溯源周期、溯源頻次;
(3)高一級計量標準(基準)量值傳遞時,已考慮到穩定性的影響;
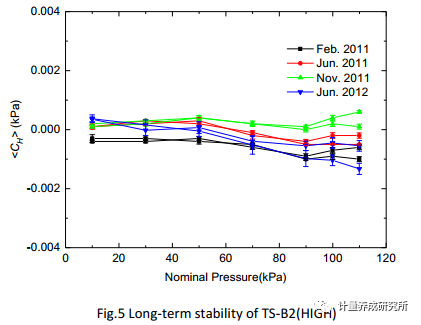

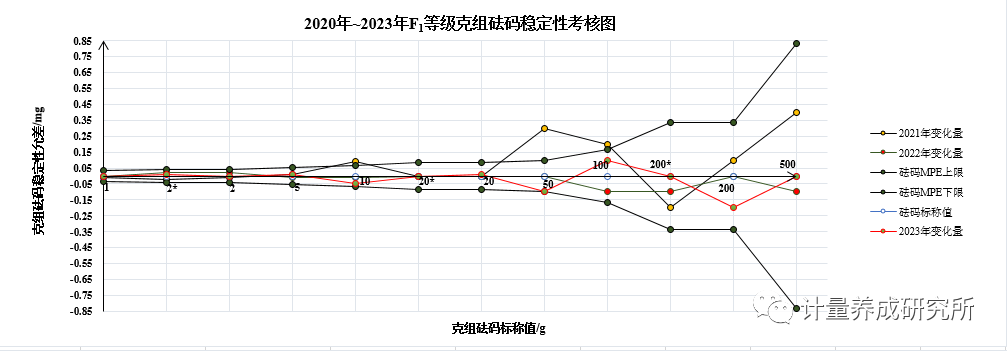
 圖4 量塊穩定性最大允許值
圖4 量塊穩定性最大允許值 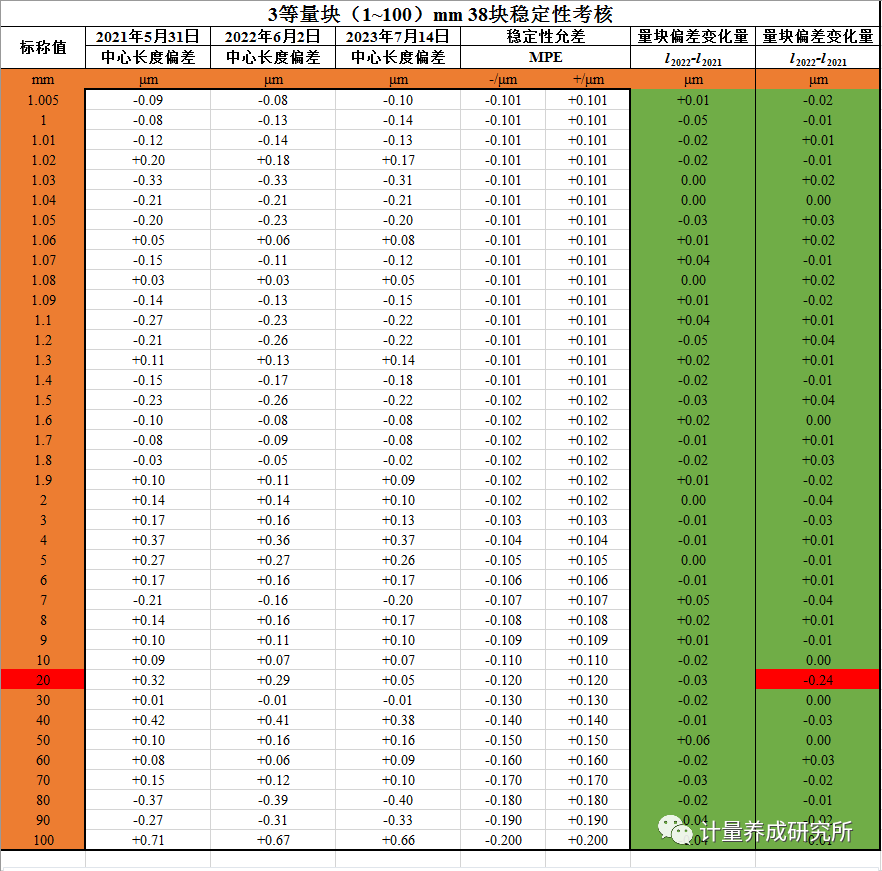



 手機:139-0495-6259
手機:139-0495-6259 座機:0415-4162867、4162868
座機:0415-4162867、4162868 郵箱:ddyibang@163.com
郵箱:ddyibang@163.com 地址:遼寧(丹東)儀器儀表產業園70-34號樓
地址:遼寧(丹東)儀器儀表產業園70-34號樓


